최소신장 트리
[참고 사이트]
https://blog.encrypted.gg/1024
https://gmlwjd9405.github.io/2018/08/28/algorithm-mst.html
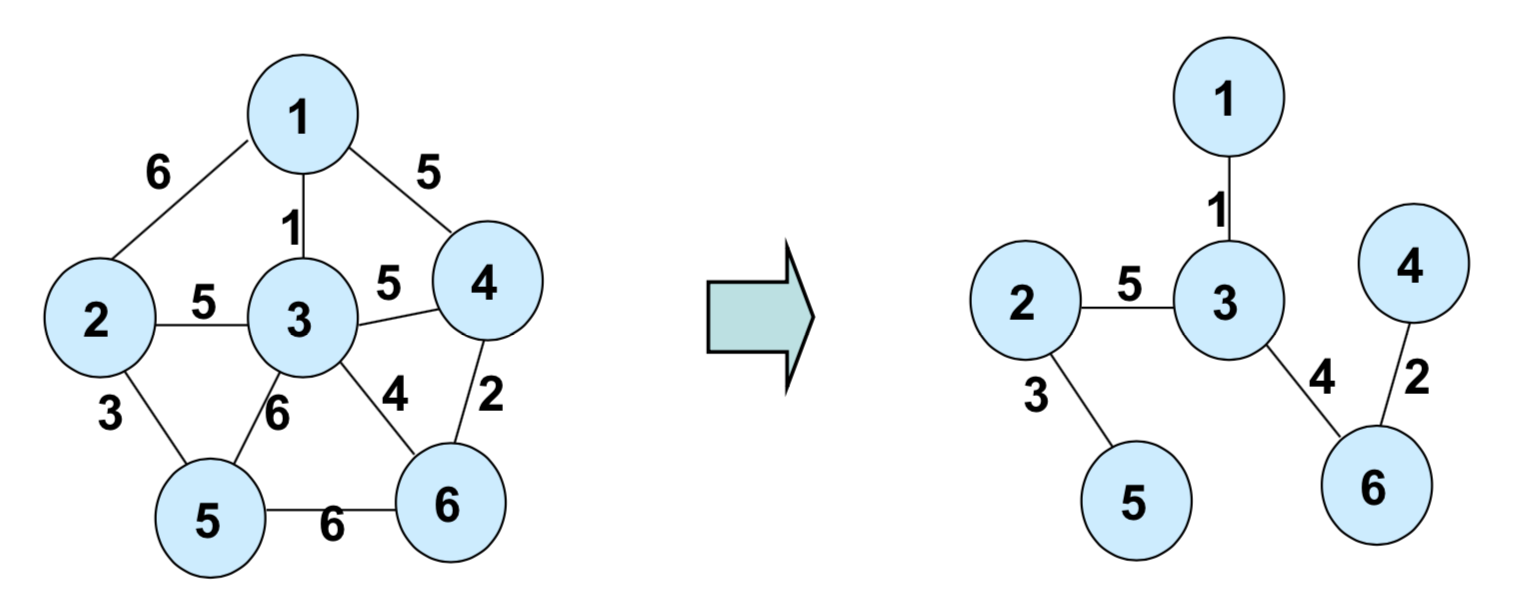
최솟값으로만 연결한 결과이다.
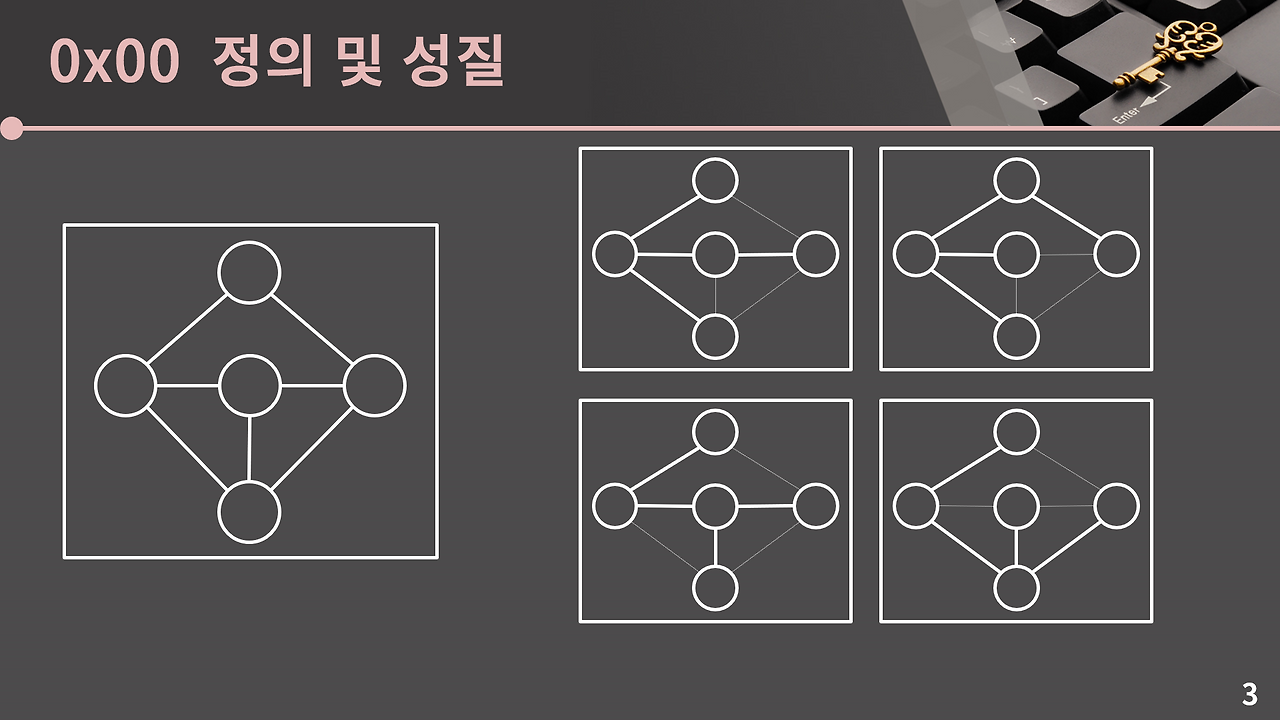
여러 형태가 있을 수도 있다.
최소신장트리
신장 트리는 주어진 방향성이 없는 그래프의 부분 그래프들 중에서 모든 정점을 포함하는 트리를 의미.
위 사진에서 오른쪽 그래프는 왼쪽 그래프의 신장 트리라고 볼 수 있습니다.
부분 그래프는 주어진 그래프에서 일부 정점과 간선만을 택해서 구성한 새로운 그래프를 의미.
→ 여기서 최소 신장 트리는 신장 트리 중에서 간선의 합이 최소인 트리를 의미. 그래프가 어떻게 생겼냐에 따라 최소 신장 트리는 여러개가 될 수 있습니다.
최소 신장 트리를 구하는 방식에는 쿠루스칼, 프림 알고리즘이 있습니다.
쿠루스칼 알고리즘
가장 비용이 낮은 간선부터 시작해 간선을 크기 순으로 살펴보며 서로 떨어져 있던 정점들을 합쳐나가서 총 V-1개의 간선을 택하는 알고리즘.
그러나 해당 알고리즘은 Unoin Find라는 알고리즘을 알아야된다고 합니다.(효율적 구성 가능)
작동순서
- 간선을 크기의 오름차순으로 정렬하고 제일 낮은 비용의 간선을 선택
- 현재 선택한 간선이 정점 u, v를 연결하는 간선이라고 할 때 만약 u, v가 같은 그룹이라면(이미 추가된 정점) 아무 것도 하지 않고 넘어감, u와 v가 다른 그룹이라면(추가되지 않은 정점) 같은 그룹으로 만들고 현재 선택한 간선을 최소 신장 트리에 추가
- 최소 신장 트리에 v-1개의 간선을 추가시켰다면 과정을 종료, 그렇지 않다면 다음으로 비용이 작은 간선을 선택한 후 2번 과정을 반복
간단히 얘기하자면, 맨처음에는 같은 정점 그룹이 없을 텐데, 간선의 크기중 가장 낮은 비용을 선택해서 같은 그룹으로 만들고 두 정점이 같은 그룹이라 생각하고 다음으로 연결할 수 있는 가장 낮은 비용을 탐색해서 같은 그룹으로 추가합니다. 만약, 이미 같은 그룹이라면 추가하지 않아도 되고 모든 정점이 같은 그룹이라면 종료합니다.
시간복잡도
구루스칼 알고리즘에서 Flood Fill방식은 시간 복잡도가 O(ElogE + VE)이고, Union Find방식은 시간 복잡도가 O(ElogE)이다. 그러므로 Union Find 방식을 써야된다고 한 것이다.
프림 알고리즘
해당 알고리즘은 우리가 배운 우선순위 큐를 알아야된다고 합니다.
작동순서
- 임의의 정점을 선택해 최소 신장 트리에 추가, 해당 정점과 연결된 모든 간선을 우선순위 큐에 추가
- 우선순위 큐에서 비용이 가장 작은 간선 선택
- 만약 해당 간선이 최소 신장 트리에 포함된 두 정점을 연결한다면 아무 것도 하지 않고 넘어감, 해당 간선이 최소 신장 트리에 포함된 정점 u와 포함되지 않은 정점 v를 연결한다면 해당 간선과 정점 v를 최소 신장 트리에 추가 후 정점 v과 최소 신장 트리에 포함되지 않는 정점을 연결하는 모든 간선을 우선순위 큐에 추가
- 최소 신장 트리에 V-1개의 간선이 추가될 때까지 2, 3번 과정 반복
간단히 얘기하자면, 아무 정점을 선택하고, 그 정점의 연결된 간선을 우선순위 큐에 추가해서 최소 신장 트리에 포함되지 않은 정점의 비용이 작은 간선을 선택한다. 최소 신장 트리에 포함되지 않은 정점이 없을때까지 해당 과정을 반복한다.
시간복잡도
각 간선이 우선순위 큐에 최대 1번씩 들어가고 삭제되므로 우선 순위큐에서 삽입, 삭제의 각각의 시간복잡도를 고려하여 시간 복잡도를 계산합니다. 각각의 삽입, 삭제 시간이 O(logE)이므로 총 복잡도는 O(ElogE)이다.
프림 알고리즘을 활용한 코드
다음은 백준 1197 최소 신장 트리를 구현한 코드입니다.
# 최소 스패닝 트리를 풀기 위해서는 크루스칼과 프림 알고리즘이 있다.
# 그러나 크루스칼은 유니온 파인드라는 이론을 알아야하기 때문에 프림 알고리즘으로 구현해봤다.
# 프림 알고리즘은 임의의 노드에서 시작해서 다음 노드중 가장 적은 비용의 간선을 찾으면서 확장합니다.
# 다음은 V 정점에 해당되는 E개의 간선 정보를 받아 합해서 최소 신장 트리의 가중치 합을 출력하는 원리의 코드이다.
import sys
import heapq
def prim(V, edges): # 입력된 정점 개수 V와 간선 값을 받는다.
# 그래프를 인접 리스트 형태로 저장 (1번 노드부터 V번 노드까지 빈 리스트 초기화)
graph = {i: [] for i in range(1, V + 1)}
# 간선 정보를 인접 리스트에 추가 u와 v는 정점 (양방향 그래프이므로)
for u, v, w in edges:
graph[u].append((v, w)) # u에서 v로 가는 간선 w
graph[v].append((u, w)) # v에서 u로 가는 간선 w
mst_weight = 0 # 최소 신장 트리의 가중치 합을 저장할 변수
visited = [False] * (V + 1) # 방문 여부 체크 리스트 (1-based index 사용, 1번부터 인덱스 시작)
priority_queue = [(0, 1)] # (가중치, 시작 노드) 형태의 우선순위 큐 (초기값: 0번 가중치로 1번 노드 시작)
while priority_queue:
weight, u = heapq.heappop(priority_queue) # 가중치가 가장 작은 간선 선택
if not visited[u]: # 해당 노드가 방문되지 않았다면
visited[u] = True # 방문 완료 처리
mst_weight += weight # 최소 신장 트리 합에 추가
# 현재 노드(u)와 연결된 간선들을 확인하여 우선순위 큐에 추가
for v, w in graph[u]:
if not visited[v]: # 아직 방문하지 않은 노드라면
heapq.heappush(priority_queue, (w, v)) # 우선순위 큐에 추가
return mst_weight # 최종 최소 신장 트리 합 리턴
# 입력 받기
V, E = map(int, sys.stdin.readline().split())
edges = [tuple(map(int, sys.stdin.readline().split())) for _ in range(E)] # 간선의 개수 E만큼 값을 받는다.(2차원 배열)
# 결과 출력
print(prim(V, edges))
# 여러 최소신장 트리 구하는 코드중에 위의 코드가 간결하고 이해하기 용이한 것 같다.
# 해당 코드들을 잘 외워보겠다.