AVL 트리

devkty 2025. 4. 21. 19:47

728x90

AVL 트리

[참고 사이트]

https://velog.io/@wakeupmakeup/AVL-%ED%8A%B8%EB%A6%AC
https://velog.io/@dankj1991/Tree-AVL-Tree
https://yoongrammer.tistory.com/72
https://www.youtube.com/watch?v=9BiHgy40NNE&ab_channel=%EC%BD%94%EB%93%9C%EB%9D%BC%EB%96%BC

AVL 트리(Adelson-Velsky and Landis Tree)는 스스로 균형을 잡는 이진 탐색 트리입니다.
균형 이진 탐색 트리(Self-balancing Binary Search Tree)의 일종으로, 트리의 높이를 항상 일정하게 유지하여 탐색, 삽입, 삭제 연산에서 O(log n)의 성능을 보장하는 자료구조입니다.

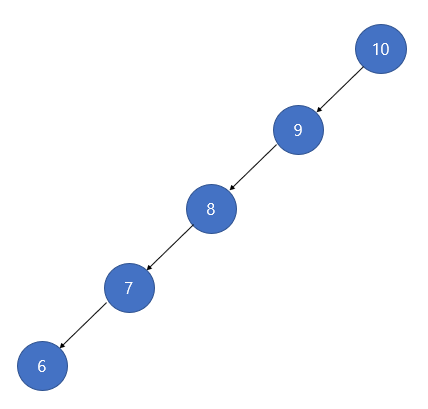
일반적인 BST는 한쪽 노드가 치우치는 상황이 생길 수 있습니다.
이런 상황에서 특정 값을 찾으면 전체 경우의 수를 찾아야하는 O(N)의 시간이 걸릴 수 있습니다.
그러므로 트리의 높이가 높아지는 단점을 방지하고자 높이 균형을 유지하는 AVL 트리를 사용합니다.
→ 높이가 2 이상이면 균형을 다시 잡습니다.

특징

이진 트리의 속성을 가진다.
균형 인수(Balance Factor)가 있다.(왼쪽 높이 - 오른쪽 높이)
AVL 트리에서는 각 노드에 대해 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이를 균형 인수라고 합니다.
균형인수는
- -1(오른쪽 서브트리의 높이가 왼쪽보다 1크다)
- 0(왼쪽과 오른쪽 서브트리의 높이가 동일함)
- 1(왼쪽 서브트리의 높이가 오른쪽보다 1크다)

을 유지해야합니다.

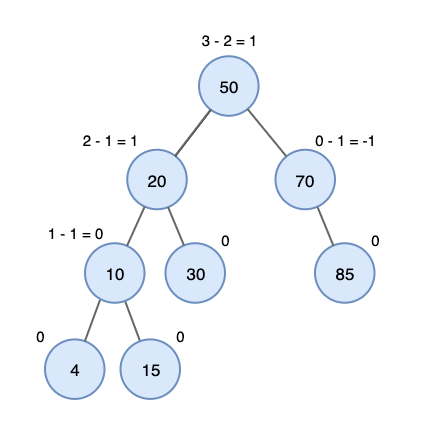
왼쪽, 오른쪽 서브 트리의 높이 차이(균형인수)가 최대 1입니다.
어떤 시점에서 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 차이를 줄입니다.
즉, 균형 인수가 2가 되면 Rotation을 통해 균형을 유지합니다.
- Ratation에는 단순 회전(LL, RR)과 이중 회전(LR, RL)이 있습니다. 자세한 회전은 밑에서 다뤄보겠습니다.
회전 연산이 추가되지만, 높이를 logN으로 유지하기 때문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN)입니다.

장단점

[장점]

트리의 균형 유지: 비균형 상태로 인해 성능이 저하되는 상황을 방지할 수 있습니다.
확실한 균형: AVL 트리는 회전 연산을 통해 항상 트리의 균형을 엄격하게 유지합니다.
O(log n)의 성능 보장: 균형을 유지하기 때문에 최악의 경우에도 탐색, 삽입, 삭제 연산이 항상 O(log n)에 이루어집니다.

[단점]

복잡한 삽입과 삭제: 균형을 맞추기 위한 회전 연산이 추가되면서 삽입과 삭제 시 일반적인 이진 탐색 트리보다 연산량이 늘어납니다.
높은 유지비용: 트리의 균형을 유지하기 위한 회전 연산은 성능이 조금 더 요구될 수 있어, 삽입/삭제가 빈번한 환경에서는 오히려 부담이 될 수 있습니다.

주요 용도

동적 데이터 관리: 삽입, 삭제가 빈번한 데이터 구조에서 성능 저하 없이 데이터를 효율적으로 관리하는 데 적합합니다.
탐색 중심 시스템: 탐색 연산이 많은 시스템에 적합하며, 특히 검색 엔진, 데이터베이스 등에서 사용됩니다.
정렬된 데이터 유지: 중위 순회를 통해 데이터를 항상 정렬된 상태로 유지할 수 있어, 실시간 정렬이 필요한 시스템에서 유용합니다.

Balance Factor(BF)

앞서 말한것처럼 Balance Factor(BF)는 외쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 값입니다.
→ Balance Factor (k) = height (left(k)) - height(right(k))

BF가 1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 높다
BF가 0이면 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같다
BF가 -1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 낮다

동작 원리

AVL 트리는 삽입(Insertion), 삭제(Deletion) 시 트리의 균형을 유지하기 위해 회전 연산을 사용합니다. 앞으로 트리의 균형이 깨졌을 때 회전으로 균형을 되찾는 과정을 설명합니다.

삽입 삭제시 노드들의 배열에 따라 4가지(LL, RR, LR, RL) 불균형이 발생할 수 있으며 각 상황마다 rotation에 방향을 달리하여 트리의 균형을 맞춥니다.

[균형이 깨지는 4가지 Case]

LL 케이스 (Left-Left): 트리의 왼쪽 자식 노드가 다시 왼쪽 자식 노드를 가지고 있는 경우.

참고로 왼쪽 자식의 BF가 0이어도 LL 케이스에 해당합니다.
즉, 왼쪽 자식의 BF가 0보다 크거나 같은 경우입니다.

RR 케이스 (Right-Right): 트리의 오른쪽 자식 노드가 다시 오른쪽 자식 노드를 가지고 있는 경우.

참고로 오른쪽 자식의 BF가 0이어도 RR 케이스에 해당합니다.
즉, 오른쪽 자식의 BF가 0보다 작거나 같은 경우입니다.

LR 케이스 (Left-Right): 트리의 왼쪽 자식 노드가 오른쪽 자식 노드를 가지고 있는 경우.

즉, 왼쪽 자식의 BF가 0보다 작은 경우입니다.

RL 케이스 (Right-Left): 트리의 오른쪽 자식 노드가 왼쪽 자식 노드를 가지고 있는 경우.

즉, 오른쪽 자식의 BF가 0보다 큰 경우입니다.

→ 각 케이스에 맞는 회전 연산을 적용하여 트리의 균형을 맞출 수 있습니다.
트리가 불균형 상태에 있을 때, 이를 해결하기 위해 단일 회전(Single Rotation) 또는 이중 회전(Double Rotation)이 사용됩니다.

다음과 같이 각 회전 케이스를 표로 정리할 수 있습니다:

회전 종류	조건(루트 노드의 BF)	자식 노드의 BF 조건	설명
LL 케이스	BF ≥ +2	왼쪽 자식의 BF ≥ 0	왼쪽 자식이 다시 왼쪽으로 치우친 경우.단순 LL 회전으로 해결.
RR 케이스	BF ≤ -2	오른쪽 자식의 BF ≤ 0	오른쪽 자식이 다시 오른쪽으로 치우친 경우.단순 RR 회전으로 해결.
LR 케이스	BF ≥ +2	왼쪽 자식의 BF < 0	왼쪽 자식이 오른쪽으로 치우친 경우.먼저 RR 회전 후, LL 회전.
RL 케이스	BF ≤ -2	오른쪽 자식의 BF > 0	오른쪽 자식이 왼쪽으로 치우친 경우.먼저 LL 회전 후, RR 회전.

회전 과정(Rotation)

LL 케이스 (Left-Left)[단일회전]

왼쪽 자식이 왼쪽 서브트리를 가지는 LL 케이스 (Left-Left)에서 불균형을 해결하는 회전입니다.
왼쪽 자식 노드가 새로운 루트가 되고, 기존의 루트 노드는 왼쪽 자식 노드의 오른쪽 자식이 됩니다.

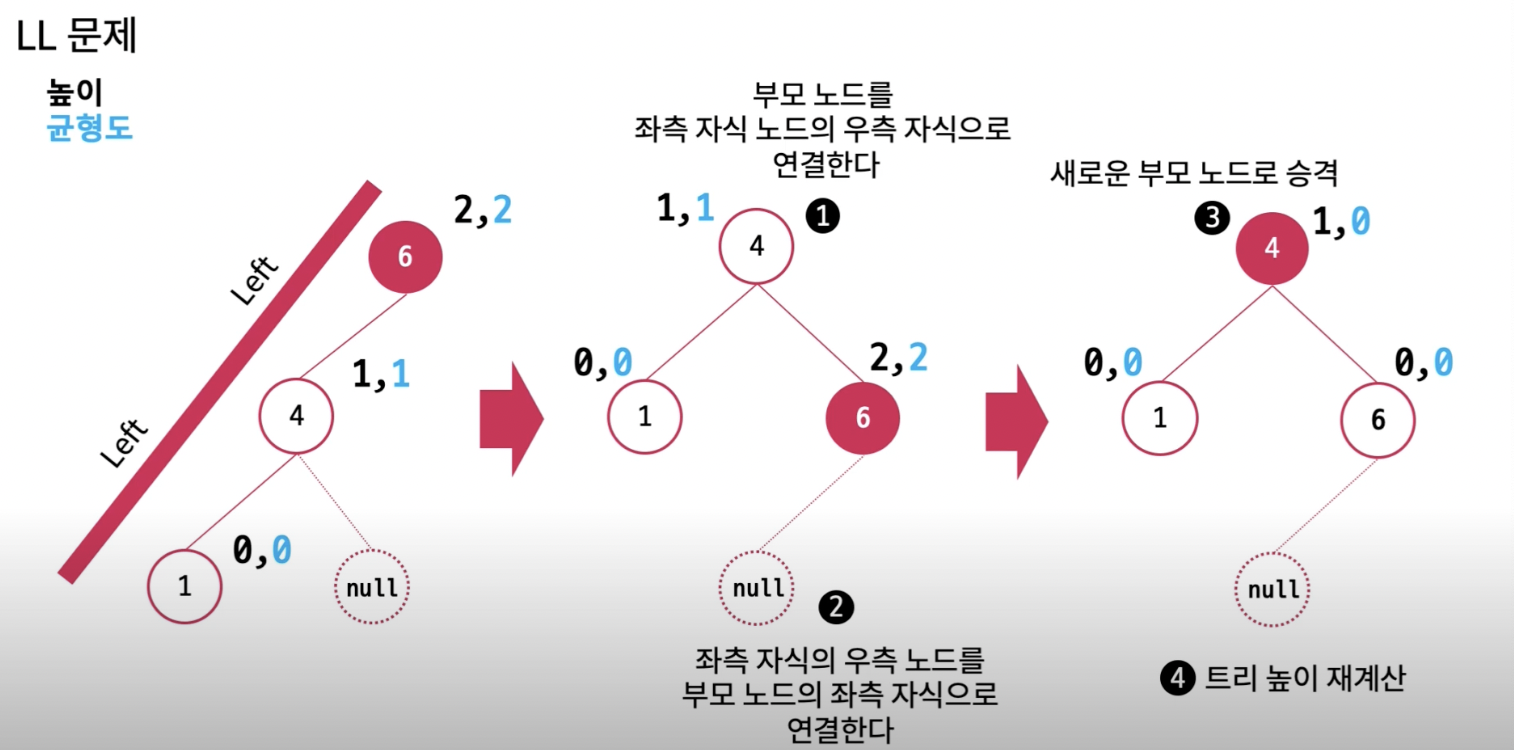
LL에서는 Right Ratation을 수행합니다.

부모 노드를 좌측 자식 노드의 우측 자식으로 연결한다.
좌측 자식의 우측 노드를 부모 노드의 좌측 자식으로 연결한다.
4를 새로운 부모로 승격시킨다.

[C언어 코드 구현]

struct node *rightRotate (struct node *z) {
  struct node *y = z->left;
  struct node *T2 = y->right;

// right 회전 수행
  y->right = z;
  z->left = T2;

// 노드 높이 갱신
  z->height = 1 + max(z->left->height, z->right->height);
  y->height = 1 + max(y->left->height, y->right->height);

// 새로운 루트 노드 y를 반환  
  return y;
}

RR 케이스 (Right-Right)[단일회전]

오른쪽 자식이 오른쪽 서브트리를 가지는 RR 케이스 (Right-Right)에서 불균형을 해결하는 회전입니다.
오른쪽 자식 노드가 새로운 루트가 되고, 기존의 루트 노드는 오른쪽 자식 노드의 왼쪽 자식이 됩니다.

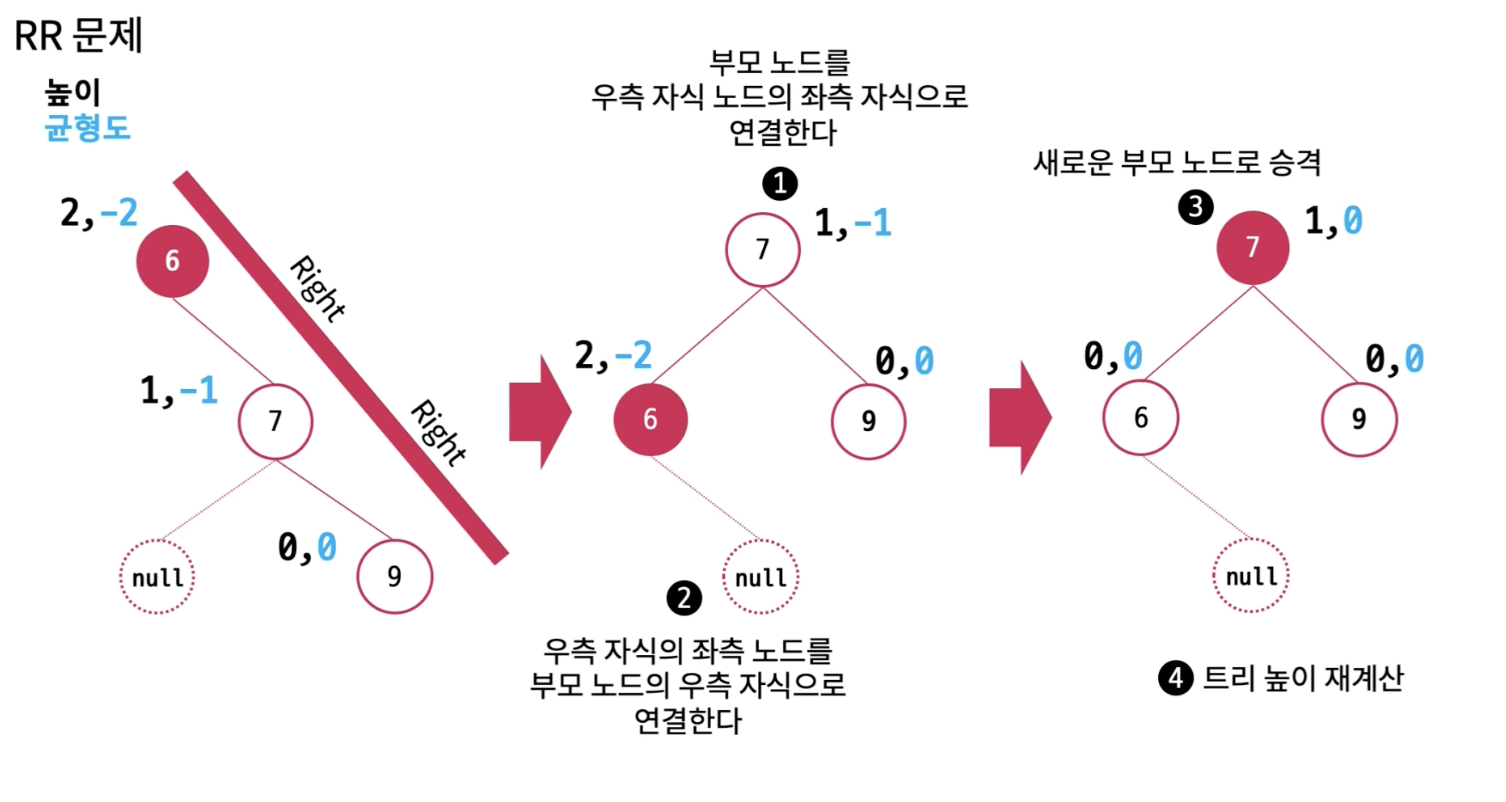
RR에서는 Left Ratation을 수행합니다.

부모 노드를 우측 자식 노드의 좌측 자식으로 연결한다.
우측 자식의 좌측 노드를 부모 노드의 우측 자식으로 연결한다.
7을 새로운 부모 노드로 승격한다.
트리 높이 재계산한다.

[C언어 코드 구현]

struct node *leftRotate (struct node *z) {
  struct node *y = z->right;
  struct node *T2 = y->left;

// left 회전 수행
  y->left = z;
  z->right = T2;

// 노드 높이 갱신
  z->height = 1 + max(z->left->height, z->right->height);
  y->height = 1 + max(y->left->height, y->right->height);

// 새로운 루트 노드 y를 반환  
  return y;
}

LR 케이스 (Left-Right)[이중 회전]

왼쪽 자식이 오른쪽 서브트리를 가지는 LR 케이스 (Left-Right)에서 불균형을 해결하는 이중 회전입니다.
먼저 왼쪽 자식의 오른쪽 서브트리에 대해 RR 회전을 수행한 후, LL 회전을 적용합니다.

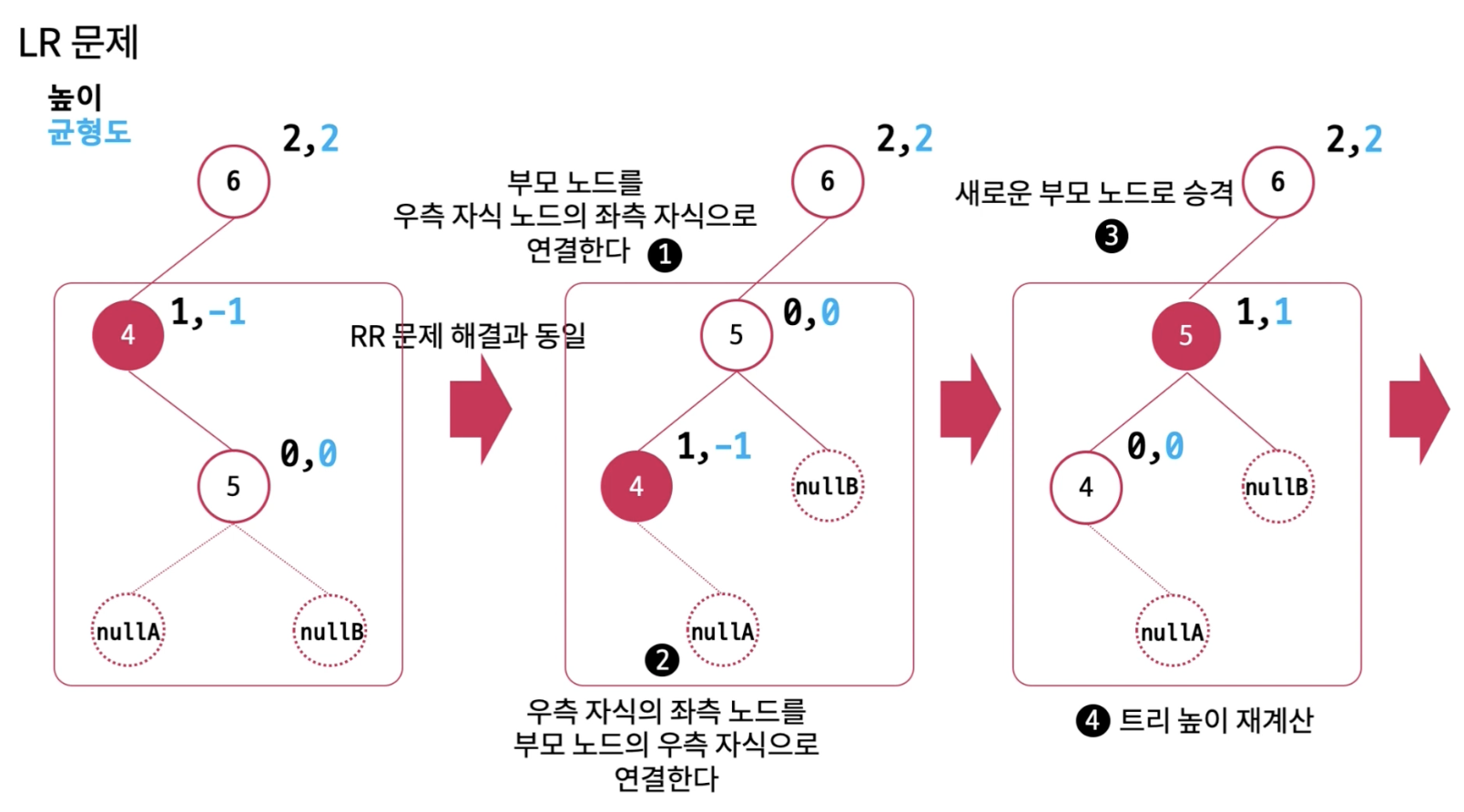
LR에서는 RR케이스를 먼저 수행하고 LL케이스를 적용합니다.

부모 노드를 우측 자식 노드의 촤측 자식으로 연결합니다.
우측 자식의 좌측 노드를 부모 노드의 우측 자식으로 연결합니다.
새로운 부모 노드로 승격합니다.
트리 높이를 재계산합니다.

[C언어 코드 구현]

y = z->left;
y = leftRotate(y);
z = rightRotate(z);

RL 케이스 (Right-Left)[이중 회전]

오른쪽 자식이 왼쪽 서브트리를 가지는 RL 케이스 (Right-Left)에서 불균형을 해결하는 이중 회전입니다.
먼저 오른쪽 자식의 왼쪽 서브트리에 대해 LL 케이스을 수행한 후, RR 케이스을 적용합니다.

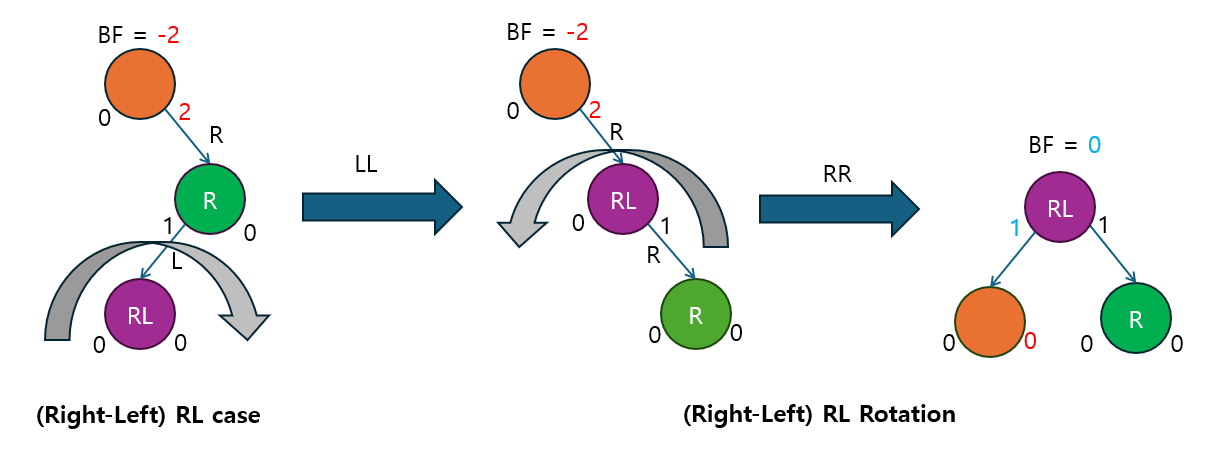
RL에서는 LL케이스를 먼저 수행하고 RR케이스를 적용합니다.
LR의 케이스와 비슷하게 총 두번의 Rotation을 통해 균형을 맞춥니다. 직접해보면서 감을 찾으면 좋을 것 같습니다.

[C언어 코드 구현]

y = z->right;
y = rightRotate(y);
z = leftRotate(z);

AVL 트리 C언어 구현

#include <stdio.h>
#include <stdlib.h>

// 노드 구조체 정의
typedef struct Node {
    int key;
    int height;
    struct Node* left;
    struct Node* right;
} Node;

// 높이 구하는 함수
int height(Node* N) {
    if (N == NULL)
        return 0;
    return N->height;
}

// 최대값 반환
int max(int a, int b) {
    return (a > b) ? a : b;
}

// 새 노드 생성 함수
Node* newNode(int key) {
    Node* node = (Node*)malloc(sizeof(Node));
    node->key = key;
    node->left = node->right = NULL;
    node->height = 1; // 새 노드는 높이 1
    return node;
}

// 오른쪽 회전
Node* rightRotate(Node* y) {
    Node* x = y->left;
    Node* T2 = x->right;

    // 회전 수행
    x->right = y;
    y->left = T2;

    // 높이 갱신
    y->height = max(height(y->left), height(y->right)) + 1;
    x->height = max(height(x->left), height(x->right)) + 1;

    return x; // 새로운 루트
}

// 왼쪽 회전
Node* leftRotate(Node* x) {
    Node* y = x->right;
    Node* T2 = y->left;

    // 회전 수행
    y->left = x;
    x->right = T2;

    // 높이 갱신
    x->height = max(height(x->left), height(x->right)) + 1;
    y->height = max(height(y->left), height(y->right)) + 1;

    return y; // 새로운 루트
}

// 균형 계수 구하기
int getBalance(Node* N) {
    if (N == NULL)
        return 0;
    return height(N->left) - height(N->right);
}

// AVL 트리 삽입 함수
Node* insert(Node* node, int key) {
    // 1. 이진 탐색 트리 삽입
    if (node == NULL)
        return newNode(key);

    if (key < node->key)
        node->left = insert(node->left, key);
    else if (key > node->key)
        node->right = insert(node->right, key);
    else // 중복 키는 허용하지 않음
        return node;

    // 2. 높이 갱신
    node->height = 1 + max(height(node->left), height(node->right));

    // 3. 균형 계수 계산
    int balance = getBalance(node);

    // 4. 균형을 맞추기 위한 회전
    // LL (왼쪽 왼쪽)
    if (balance > 1 && key < node->left->key)
        return rightRotate(node);

    // RR (오른쪽 오른쪽)
    if (balance < -1 && key > node->right->key)
        return leftRotate(node);

    // LR (왼쪽 오른쪽)
    if (balance > 1 && key > node->left->key) {
        node->left = leftRotate(node->left);
        return rightRotate(node);
    }

    // RL (오른쪽 왼쪽)
    if (balance < -1 && key < node->right->key) {
        node->right = rightRotate(node->right);
        return leftRotate(node);
    }

    return node;
}

// 중위 순회 (정렬된 출력)
void inorder(Node* root) {
    if (root != NULL) {
        inorder(root->left);
        printf("%d ", root->key);
        inorder(root->right);
    }
}

// 메인 함수
int main() {
    Node* root = NULL;

    // 예제 입력
    int keys[] = {10, 20, 30, 40, 50, 25};
    int n = sizeof(keys) / sizeof(keys[0]);

    for (int i = 0; i < n; i++)
        root = insert(root, keys[i]);

    printf("중위 순회 결과 (정렬된 키): ");
    inorder(root);
    printf("\n");

    return 0;
}

해당 과정을 더 상세히 보고 싶으면 아래의 벨로그를 들어가서 확인해 봅시다.(삽입, 삭제 등)
https://velog.io/@dankj1991/Tree-AVL-Tree

728x90