728x90
[참고 사이트]
다익스트라 알고리즘
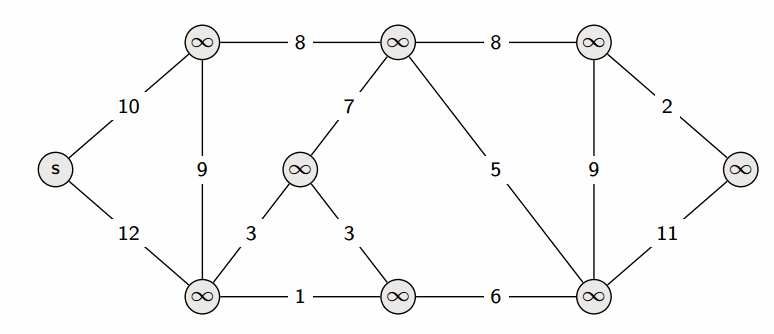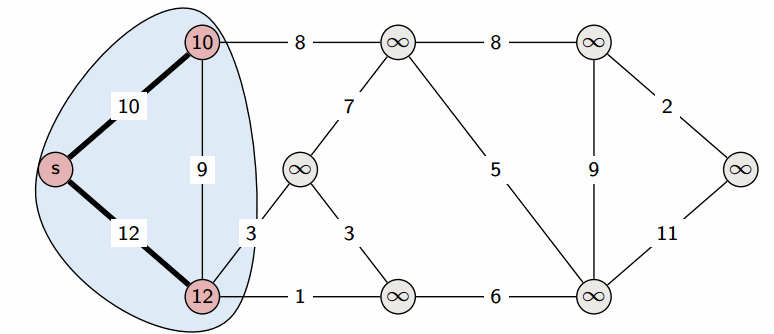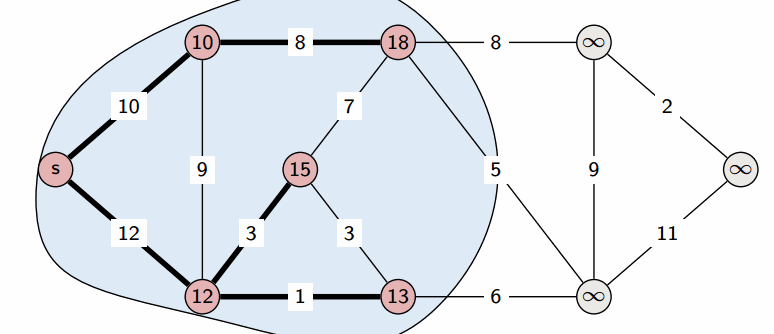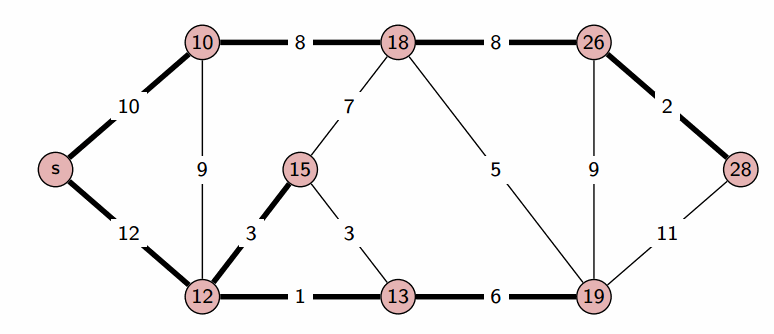
방향 그래프 혹은 무방향 그래프에서 하나의 시작점으로부터 다른 모든 정점까지의 최단 거리를 구해주는 알고리즘. 매번 최단 거리를 갱신한다.(우선 순위 큐 기준)
현재까지 발견한 가장 짧은 경로를 우선 선택하여 진행하는 그리디 알고리즘.
작동순서(우선순위 큐)
- 우선 순위 큐에 (0,시작점) 추가
- 우선 순위 큐에서 거리가 가장 작은 원소를 선택, 해당 거리가 최단 거리 테이블에 있는 값과 다를 경우 3번 과정을 수행하지 않고 넘어감
- 원소가 가리키는 정점: v, v와 이웃한 정점들에 대해 최단 거리 테이블 값보다 v를 거쳐가는 것이 더 작은 값을 가질 경우 최단 거리 테이블의 값을 갱신하고 우선순위 큐에(거리, 이웃한 정점의 번호) 추가
- 우선순위 큐가 빌 때까지 2, 3번 과정을 반복
특징
- 한 번 처리한 노드는 최단 거리 값이 확정된다.
- 음수 간선이 하나라도 있으면 사용할 수 없음.(위의 특징처럼 한 번 처리한 노드는 최단 거리 값이 확정되는데, 다른 쪽에 음수 간선이 있으면 해당 전제가 깨지게되어 원칙이 무너진다. 그래서 최단 거리를 구할 수도 있고 안구할 수도 있다.)
- 순차탐색과 우선순위 큐 방식 두개를 사용할 수 있다.(순차 탐색의 경우 방문 여부를 기록해야한다.)
- 우선 순위 같은 경우 최단 거리의 노드를 앞으로 정렬하여 기존 최단 거리보다 크면 무시한다.
- 파이썬에서 heapq와 priority queue를 통해 구현 가능하다.( 힙큐를 쓰는 이유는 병목현상을 배제하기 위해서 우전적으로 쓴다 병목현상 배제와 메모리 절약)
- 시간 복잡도는 우선순위 큐에서 최악의 경우 O(ElogV)이다.
- 네트워크 쪽에서 많이 쓴다.
코드는 완벽히 이해 후 수정하겠다.
밑에 코드는 1753 최단경로 코드이다.
import sys
import heapq
INF = float('inf') # 무한대를 의미하는 값 설정
def dijkstra(V, E, start, edges):
# 그래프를 인접 리스트로 표현 (1번 노드부터 시작)
graph = {i: [] for i in range(1, V + 1)}
for u, v, w in edges:
graph[u].append((w, v)) # u라는 기준점에서 (가중치, 목적지 노드)형태로 값 저장
# 최단 거리 테이블 초기화
distance = [INF] * (V + 1) # 모두 무한으로 초기화(그래야 비교해서 교체 가능, 0이면 안되므로)
distance[start] = 0 # 시작 정점의 거리는 0
# 우선순위 큐 (최소 힙) 사용
pq = [(0, start)] # (현재까지의 거리, 정점)
while pq:
cur_dist, cur_node = heapq.heappop(pq) # 최단 거리 노드 선택
if distance[cur_node] < cur_dist:
continue # 이미 처리된 노드라면 무시
# 현재 노드의 인접 노드 확인
for nxt_dist, nxt_node in graph[cur_node]:
new_dist = cur_dist + nxt_dist
if new_dist < distance[nxt_node]: # 더 짧은 경로 발견 시 갱신
distance[nxt_node] = new_dist
heapq.heappush(pq, (new_dist, nxt_node)) # 우선순위 큐에 추가
return distance
# 입력 받기
V, E = map(int, sys.stdin.readline().split()) # 정점 수 V, 간선 수 E
start = int(sys.stdin.readline()) # 시작 정점
edges = [tuple(map(int, sys.stdin.readline().split())) for _ in range(E)] # 간선 정보 입력
# 다익스트라 실행 및 결과 출력
distances = dijkstra(V, E, start, edges)
for i in range(1, V + 1):
print("INF" if distances[i] == INF else distances[i])+ [추가사항] 직관적인 구현 순서
추가적인 공부를 하면서 헷갈려서 내용을 추가한다. 직관적으로 구현 순서를 정리했다.
시작지점에서 인접 노드 최단거리 확인 → 방문하지 않은 노드중 최단 거리가 가장 짧은 노드 선택 → 해당 노드에서의 인접노드 최단 거리 탐색 → 방문하지 않은 노드중 최단 거리가 가장 짧은 노드 선택 → 반복 → 최종 목적지 노드의 짧은 거리 탐색하여 찾으면 종료
728x90
'크래프톤 정글(알고리즘 주차 WEEK 0 ~ 4)' 카테고리의 다른 글
| B-Tree (0) | 2025.04.03 |
|---|---|
| WEEK 3 컴퓨터 시스템 공부 (0) | 2025.04.03 |
| 최소신장 트리 (0) | 2025.04.03 |
| WEEK 03 알고리즘 TIL(3월31일 월요일) (0) | 2025.04.03 |
| WEEK 03 알고리즘 여담(3월30일 일요일) (0) | 2025.04.03 |