B-Tree
[참고 사이트]
https://yeongjaekong.tistory.com/38
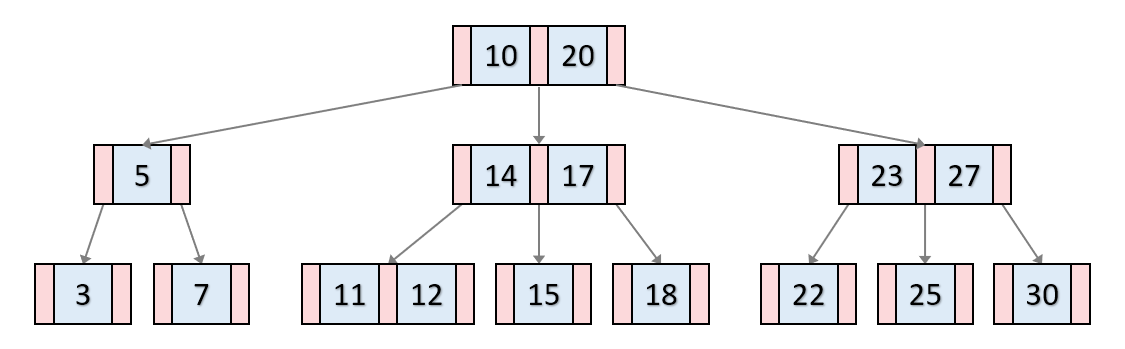
최대 3개의 키와 4개의 자식을 가질수 있는 차수가 3인 B-Tree
B-Tree
B-Tree는 이진트리에서 발전되어 모든 리프노드들이 같은 레벨을 가질 수 있도록 자동으로 균형을 맞추는 트리입니다. 정렬된 순서를 보장하고 멀티레벨 인덱싱을 통한 빠른 검색을 할 수 있기 때문에 DB에서 사용하는 자료구조 중 한 종류라고 합니다. B-Tree뿐아니라 B+Tree도 존재합니다.
B트리는 이진트리와 다르게 하나의 노드에 많은 수의 정보를 가지고 있을 수 있습니다. 최대 N개의 자식을 가질 수 있는 B트리를 N차 B트리라고 합니다.
특징
- 노드는 최대 M개 부터 M/2개 까지의 자식을 가질 수 있습니다.
- 노드에는 최대 M−1개 부터 [M/2]−1개의 키가 포함될 수 있습니다.
- 노드의 키가 x개라면 자식의 수는 x+1개 입니다.
- 최소차수는 자식수의 하한값을 의미하며, 최소차수가 t라면 M=2t−1을 만족합니다. (최소차수 t가 2라면 3차 B트리이며, key의 하한은 1개입니다.)
- 탐색, 삽입, 삭제 모두 가능한 트리입니다.
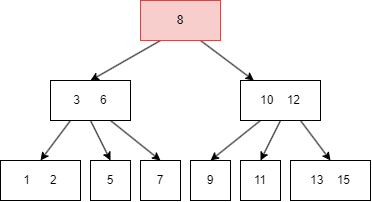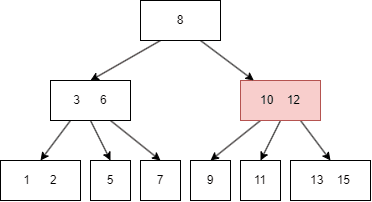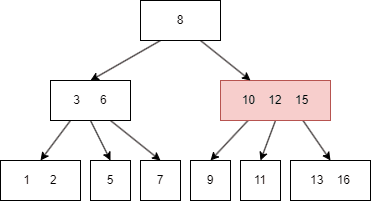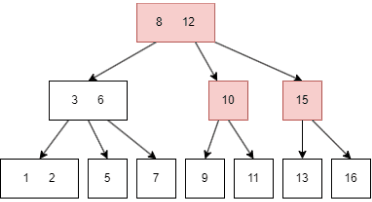
B-Tree 과정을 일일이 설명할 수 없으므로 상단의 블로그를 참고해서 이해하면 될 것이다.
파이썬 코드 또한 상단의 블로그에 잘 기술되어 있어 참고하면 될 것이다.
[중요!] Big O 데이터 시간 복잡도에 대해서
보통 DB에서 자주 사용하는 트리이다. 큰 양의 정렬된 데이터를 관리하는 DB특성상 B-Tree를 사용하면 데이터 검색 성능이 향상될 수 있습니다. B-Tree인덱스를 사용할 때와 사용하지 않을 때(Tree 등) 데이터 검색 시간 복잡도를 Big O 표기법을 활용하여 비교하고 설명해보겠습니다.
→ B-Tree 인덱스를 사용할 때의 데이터 검색 시간 복잡도는 O(logN)이다. 여기서 N은 DB 내의 레코드 수입니다. B-Tree 구조는 균형 이진 트리와 유사하므로 데이터를 효율적으로 검색할 수 있습니다.
반면, B-Tree 인덱스를 사용하지 않을 경우 선형 검색을 수행하므로 검색시간 복잡도는 O(N)이 됩니다. (모든 데이터 확인) 따라서, 데이터 양이 많을수록 B-Tree인덱스를 사용하는 것이 성능 면에서 훨씬 유리합니다.
'크래프톤 정글(알고리즘 주차 WEEK 0 ~ 4)' 카테고리의 다른 글
| WEEK 03 알고리즘 TIL(4월2일 수요일) (0) | 2025.04.03 |
|---|---|
| WEEK 03 알고리즘 TIL(4월1일 화요일) (1) | 2025.04.03 |
| WEEK 3 컴퓨터 시스템 공부 (0) | 2025.04.03 |
| 다익스트라 알고리즘 (0) | 2025.04.03 |
| 최소신장 트리 (0) | 2025.04.03 |